Cho hàm số \(f(x) = {3^x} \cdot \ln x\)
Quảng cáo
Trả lời:
a) Sai.
Điều kiện xác định của \(\ln x\) là \(x > 0\) . Vậy, tập xác định của hàm số là \(D = (0; + \infty )\).
b) Sai.
Ta áp dụng công thức đạo hàm của tích \((u \cdot v)' = u'v + uv'\), với \(u = {3^x}\) và \(v = \ln x\).
+) \(u' = {({3^x})^\prime } = {3^x} \cdot \ln 3\)
+) \(v' = {(\ln x)^\prime } = \frac{1}{x}\)
Đạo hàm \(f'(x)\) là: \(f'(x) = {({3^x})^\prime } \cdot \ln x + {3^x} \cdot {(\ln x)^\prime } = ({3^x} \cdot \ln 3) \cdot \ln x + {3^x} \cdot \frac{1}{x}\)\( = {3^x}\left( {\ln 3 \cdot \ln x + \frac{1}{x}} \right)\)
c) Đúng.
Để xét tính đơn điệu, ta cần xét dấu của đạo hàm \(f'(x) = {3^x}\left( {\ln 3 \cdot \ln x + \frac{1}{x}} \right)\) trên \((3; + \infty )\):
+) \({3^x} > 0\) với mọi \(x \in (3; + \infty )\).
+) \(\frac{1}{x} > 0\) với mọi \(x \in (3; + \infty )\).
+) \(\ln 3 > 0\) (vì \(3 > 1\)).
+) Trên \((3; + \infty )\), ta có \(x > 3 > e\). Do đó \(\ln x > \ln 3 > 1 > 0\) .
Vì tất cả các thừa số và số hạng trong ngoặc đều dương trên \((3; + \infty )\), ta có:
\(f'(x) = {3^x}\left( {\ln 3 \cdot \ln x + \frac{1}{x}} \right) > 0\,,\forall x \in (3; + \infty )\)
Do đó, hàm số đồng biến trên \((3; + \infty )\).
d) Sai.
\[{3^{{y^2} - \frac{{|x|}}{x}}} \le {\log _{{y^2} + 3}}\left( {\frac{{|x|}}{3} + 3} \right) \Leftrightarrow \frac{{{3^{{y^2} + 3}}}}{{{3^{\frac{{|x|}}{3} + 3}}}} \le \frac{{\ln \left( {\frac{{|x|}}{3} + 3} \right)}}{{\ln \left( {{y^2} + 3} \right)}} \Leftrightarrow {3^{{y^2} + 3}}\ln \left( {{y^2} + 3} \right) \le {3^{\frac{{|x|}}{3} + 3}}\ln \left( {\frac{{|x|}}{3} + 3} \right)\,\,\,\left( * \right)\]
Do hàm \(f(x) = {3^x} \cdot \ln x\) đồng biến trên \((3; + \infty )\) nên \[\left( * \right) \Leftrightarrow {y^2} + 3 \le \frac{{|x|}}{3} + 3 \Leftrightarrow {y^2} \le \frac{{\left| x \right|}}{3}\] .
Ta thấy chỉ có 3 trường hợp đó là \[{y^2} \le 1\],\[{y^2} \le 2\],\[{y^2} \le 3\] mã mỗi trường hợp có đúng \(3\) số ngyên \(y\) thỏa mãn.
Trường hợp 1 ứng với \[\frac{{\left| x \right|}}{3} = 1 \Leftrightarrow x = \pm 3\].
Trường hợp 2 ứng với \[\frac{{\left| x \right|}}{3} = 2 \Leftrightarrow x = \pm 6\].
Trường hợp 2 ứng với \[\frac{{\left| x \right|}}{3} = 3 \Leftrightarrow x = \pm 9\].
Vậy có \(6\) số nguyên \(x\) sao cho ứng với mỗi số nguyên \(x\) có đúng 3 số nguyên \(y\) thỏa mãn bất phương trình: \({3^{{y^2} - \frac{{|x|}}{x}}} \le {\log _{{y^2} + 3}}\left( {\frac{{|x|}}{3} + 3} \right)\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \[1,5\].
. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/22-1766969244.png)
Gọi \[O\] là tâm đường tròn \[(R = 1)\]; \[K\] là điểm giữa đường tròn và đường thẳng; \[H\] là hình chiếu của \[P\] lên \[OK\]. Có \[PH = 2\;km\]; \[OH = OK + KH = 1 + 0,5 = 1,5\;km\]; \[OP = \sqrt {{2^2} + 1,{5^2}} = 2,5\;km\].
Dễ thấy vị trí \[Q\] để cho \[PQ\] ngắn nhất là \[P,Q,O\] thẳng hàng.
Khi đó \[\min PQ = OP - R = 2,5 - 1 = 1,5\;km\].
Lời giải
Đáp án: \(3969\).
Xếp 10 người thành một hàng ngang ta có \(10!\) cách xếp.
Khi xếp 10 người thành 1 hàng, giữa 10 người có 9 vách ngăn. Để chia 10 người thành 4 nhóm ta cần chọn 3 vách ngăn trong 9 vách ngăn là \(C_9^3\).
Xếp 4 nhóm vừa chia vào 4 ga ta có \(4!\) cách xếp.
Vậy số cách 10 hành khách đang đứng đợi ở sân ga lên tàu QH15 là: \(T = 10!.C_9^3.4!\).
Vậy \(\frac{T}{{76800}} = \frac{{10!.C_9^3.4!}}{{76800}} = 3969\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
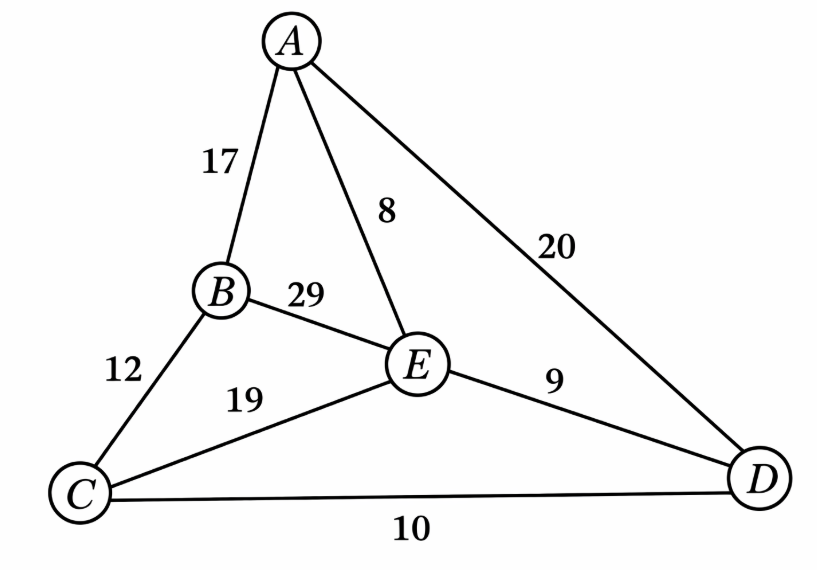
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/21-1766969228.png)